Regular inference is the task of inferring a deterministic finite-state automaton (DFA) from a training set of positive strings and negative strings which, respectively, belong and do not belong to a regular language. Additionally, the regular inference task is usually formulated as finding the minimum-state DFA that is consistent with the training data. This problem is NP-complete and is one of the more intensely studied areas in the broader field of grammatical inference.
One of the most successful approaches in addressing the problem is to apply so-called state-merging algorithms. A highly specific hypothesis called a prefix-tree acceptor (PTA) is created from the training data, allowing pairs of states to be iteratively selected and merged to compact and generalise the hypothesis.
Another interesting approach consists in reducing this problem to Boolean satisfiability (SAT). Here, the PTA is reduced to an instance of graph colouring which, in turn, is reduced to SAT. The generated clauses are then passed to an SAT solver and the subsequent truth assignment is used to construct a solution. This exact algorithm results in millions of clauses on large problems, which prove to be too much for SAT solvers. Therefore, the PTA is first preprocessed using a state-merging algorithm, such as EDSM, to obtain a partially identified DFA, used as an input in the reduction to SAT. This greatly diminishes the size of the encoding at the cost of no longer being an
exact algorithm due to any possible incorrect merges performed during preprocessing.
This project has set out to test the DFA-SAT algorithm, performing a comparative analysis on Abbadingo and Stamina problem instances. DFA-SAT was compared with current state-of-the-art state-merging algorithms, in which a library of DFA instances was created. This was used in comparing DFA-SAT against EDSM, windowed EDSM, and BlueFringe. The study also proposes ideas for other preprocessing methods.
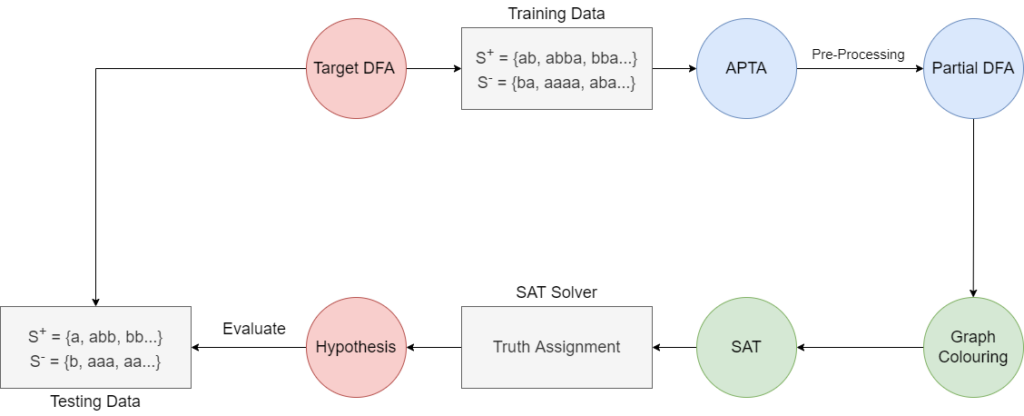
of a target DFA; the PTA is preprocessed and the partial DFA is then
reduced to graph colouring, and then SAT. The truth assignment then
offers a hypothesis to be evaluated with the testing data
Student: Logan Formosa
Course: B.Sc. IT (Hons.) Artificial Intelligence
Supervisor: Dr Kristian Guillaumier
Co-Supervisor: Prof. John Abela
