Determining feasible routing paths is a substantial challenge in the humanitarian aid, civil, military, and commercial spheres. Specifically, finding a tour on a road network is a principal concern in planning logistics. The essence of this problem is characterized by the Travelling Salesman Problem (TSP). In a TSP, the salesman visits all cities exactly once. Joining the last city with the starting one produces a Hamiltonian cycle on the cities. One of the many applications of TSP is the Green Vehicle Routing Problem which considers fuel tank capacity and refueling stops [1].
This study proposes a new effective approach that utilizes a Quad-Tree plane partitioning algorithm. Firstly, the Quad-Tree algorithm embeds all tour nodes along a plane. It then recursively partitions them into squares until each square contains at most three nodes. Secondly, the nodes within each square are repeatedly connected with each other in a bottom-up approach. The algorithm starts with the nodes in the smallest squares at the lowest level
of the partitioning and works in a bottom-up approach until it reaches the largest child square of the Quad-Tree parent. This gives a Hamiltonian Cycle of the nodes (cities). This approach produces an approximation to the optimal tour length of the given nodes in polynomial time, thus becoming a quad-tree polynomial-time approximation scheme (PTAS). The final step of the study involves comparing this Quad-Tree PTAS with another sample solution based on a Genetic Algorithm (GA) approach.
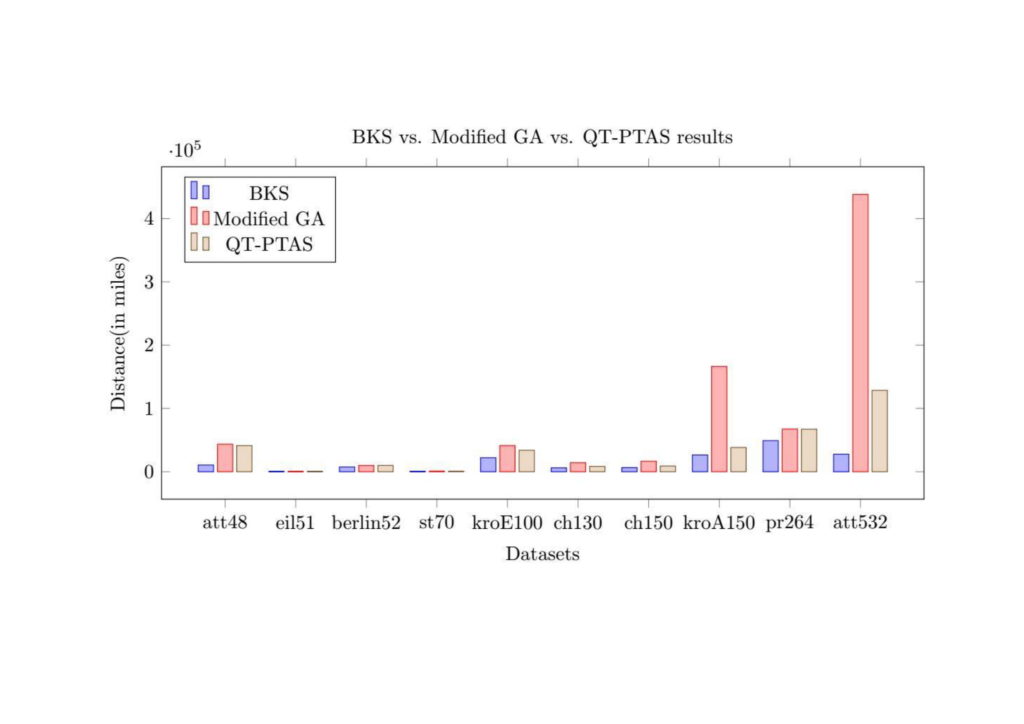
The experiments are performed on ten real-life datasets of varying sizes. All the datasets are passed through the two approaches and the outcomes are analysed. The results obtained show that, in these experiments, the Quad-Tree PTAS consistently outperforms the GA in terms of tour length cost and computational time. The improvement in cost and time and the effectiveness of the Quad-Tree PTAS when compared to the GA approach grows with the size of the dataset. This may indicate that this improvement would increase with larger datasets. Therefore, the proposed Quad-Tree PTAS approach holds promise when compared with the Genetic Algorithm meta-heuristic and may be applied effectively to other problem domains.
Figure 2. Genetic Algorithm (GA) vs Quad-Tree Polynomial-Time Approximation Scheme (QT-PTAS) results
References/Bibliography:
[1] S. Erdoğan and E. Miller-Hooks, “A Green Vehicle Routing Problem,” Transportation research part E: logistics and transportation reciew, vol. 48, no.1, pp. 100-114, 2012.
Student: Nikola Glushkov
Course: B.Sc. IT (Hons.) Computing and Business
Supervisor: Dr. Michel Camilleri
Co-supervisor: Dr. John Abela
