Arithmetic operations on very large integers are used in many applications such as computer algebra, computational number theory and public-key cryptography. A drawback is that most computers are typically built with a word size of 32 or 64 bits, which means that a machine register can only hold integers up to a maximum value of 2^64-1 for unsigned numbers. A solution would be to use multi-precision arithmetic libraries, which would allow numbers of any size. However, increasing the size of the numbers would also increase the amount of work required to perform the necessary arithmetic. Since a central processing unit (CPU) might struggle to keep up with the complexity of these computations, a graphics processing unit (GPU) could be used to offload some of the work from the CPU. GPUs and have been deemed to be useful in high-performance computing due to their substantial parallel architecture of hundreds to thousands of arithmetic units.
In this project, a parallel version of the addition, subtraction and multiplication operations for large

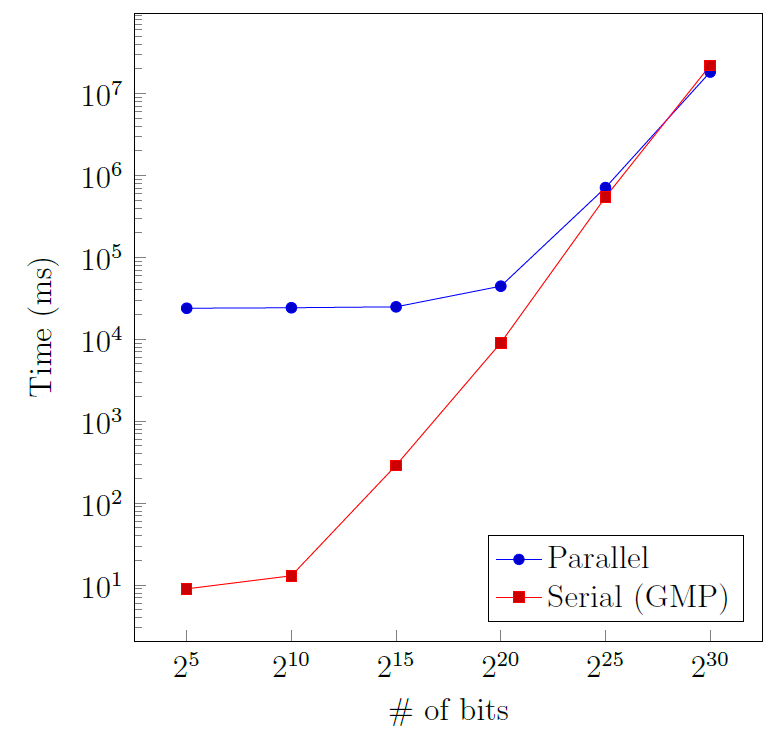
numbers was implemented on a GPU. The addition was implemented using the prefix-parallel technique, which has been used on a smaller scale in the carry-lookahead adder [1]. This technique offers greater efficiency when executed on a large number of processors. For the multiplication, a warp-synchronous approach was adopted [2], taking advantage of how the thread grouping was done in the GPU. For multiplications of even larger numbers, the Karatsuba algorithm was chosen. The parallel implementation was tested on an NVIDIA GeForce GTX 1050 (Figure 1) and compared with the GNU Multiple Precision Arithmetic Library (GMP), which runs on a CPU. For numbers of 2^30 bits, a speed-up of 1.7 was achieved for the addition operation (Figure 2). Furthermore, the multiplication operation achieved up to 2.6 speed-up for 1024-bit numbers when fully utilising the GPU.
References/Bibliography:
[1] A. Weinberger and J. Smith, “A one-microsecond adder using one-megacycle circuitry,” IRE Transactions on Electronic Computers, no. 2, pp. 65-73, 1956.
[2] T. Honda, Y. Ito, and K. Nakano, “GPU-accelerated bulk execution of multiple-length multiplication with warp-synchronous programming technique,” IEICE TRANSACTIONS on Information and Systems, vol. 99, no. 12, pp. 3004-3012, 2016.
Student: Gerard Tabone
Course: B.Sc. IT (Hons.) Computing Science
Supervisor: Prof. Johann A. Briffa
