A clique in an undirected graph is a subset of the vertices, such that every two distinct vertices would be adjacent to each other. Being a proven NP-hard problem, the maximum clique problem (MCP) entails finding the largest clique in a graph, which could then be applied to other areas such as: bioinformatics, social network analysis, network security, among others.
Since the MCP is an NP-hard problem, exact algorithms that would invariably find the maximum clique in a graph are not always tractable, and approximation would be required in graphs that tend to have a large search space. Hence, this project was dedicated to investigating the use of genetic algorithms (GAs) to approximate the MCP. The main objective was to ascertain whether the application of GAs would be a suitable search technique for this particular problem by comparing it with other types of algorithms, in particular a Monte Carlo (MC) search.
Pseudocode of GAs for the MCP already existed in literature. Therefore, the project reproduced the bulk of the results from one of the best-performing GAs. In addition, an MC-based search was developed, with experiments from this algorithm being duly recorded. In the interest of impartiality, both algorithms were run for the same number of times, to the same number of chromosomes in each run, meaning that the number of solutions explored by both algorithms was the same. Furthermore, runs were based on the DIMACS dataset, which is the main dataset used for problems related to the MCP.
Results from both algorithms were carefully compared and evaluated. The outcome of this task indicated that the MC algorithm slightly outperformed the GA. However, in most of the instances where the same maximum clique was found, the MC algorithm found the result in a smaller number of generated chromosomes. This suggests that stochasticity is equally satisfactory as recombination (crossover) when approximating the MCP.
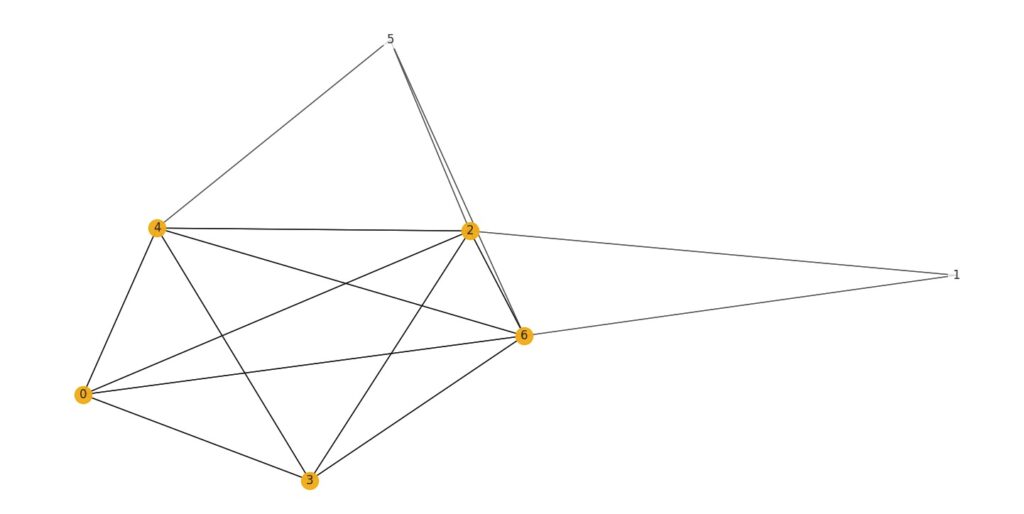
Figure 1. An example of a maximum clique in a graph
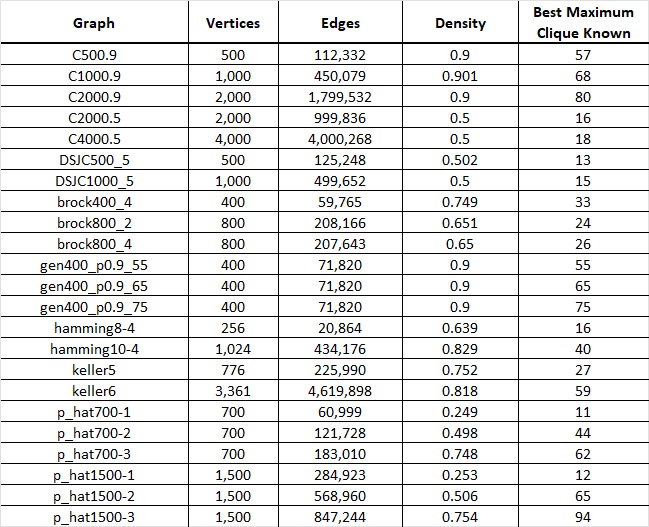
Figure 2. Table displaying a subset of graphs from the DIMACS dataset
Student: Michael Vella
Supervisor : Prof. John Abela
